A green paper
[*]
by Casey Detrio
July 2015
Smart Markets for Stablecoins
Providing Liquidity on Blockchains with Decentralized Autonomous Market Makers for Combinatorial Portfolios
(quick-and-dirty version)
This document aims to provide explorable examples. Included below are three interactive charts:
1. Portfolios of Binary Options
2. Combinatorial Auctioneer
3. Automated Market Maker
Abstract
[*]
Mechanisms designed to create stable-value cryptoassets, or "stablecoins", can be categorized as two basic types: (1) monetary policy schemes, and (2) hedging strategies. Monetary policy schemes attempt to stabilize price by adjusting coin supply, while hedging strategies stabilize value by transferring price volatility risk from hedgers to speculators. Both types ultimately depend on market liquidity; without sufficient liquidity, neither type is viable. To enhance liquidity, we propose the use of two “smart market”[*] mechanisms: (1) combinatorial auctions with batch processing, or batch combinatorial auctions; and (2) automated market makers[*].
Combinatorial auctions aggregate liquidity by enabling multiple securities to be traded together in bundles and matched multilaterally on a combinatorial order book. Combinatorial auctions also integrate prices, improving the welfare of average traders since arbitrage-freeness or the "law of one price" is enforced by the mechanism itself rather than by advanced traders' exploitation of arbitrage opportunities. Batch processing further aggregates liquidity by enabling multiple traders to transact simultaneously at a uniform clearing price. Batch processing not only reduces traders' reliance on market makers, it also eliminates the high-frequency trading arms race by preventing traders with a tiny speed advantage from earning mechanical arbitrage profits.
An automated market maker (AMM) acts as a default liquidity provider or "market maker of last resort". An AMM also has an additional purpose: in conjuction with a combinatorial auction, it serves as a mathematical technique for calculating unique optimal clearing prices. We call an AMM programmed into a blockchain smart contract a decentralized autonomous market maker (DAMM). A DAMM is obligated by the p2p network executing its source code to hold funds in reserve for later redeemability, and to continue providing liquidity to the best of its ability regardless of market conditions.
To motivate the adoption of these two smart market mechanisms, we present an example combinatorial derivatives market for hedging and speculating on the future price of a digital currency such as bitcoin. In the example, traders use portfolios of binary options to construct synthetic positions that replicate the payoffs of conventional derivatives, such as options and futures. The advantage of trading these synthetic positions compared to conventional derivatives is that the combinatorial market structure enables all synthetic positions to be matched multilaterally in a unified pool of liquidity. Thus, trading synthetic positions on a combinatorial order book enhances liquidity, gives traders greater leverage and reduces their transaction costs.
The features and guarantees of batch combinatorial auctions and DAMMs should help jump-start liquidity, reduce spreads, prevent "flash crashes", and ensure price convergence.
0 Introduction: From Legacy Institutions to Smart Markets
The most widely used method for trading securities is the continuous double auction (CDA). The CDA is a legacy institution[n] inherited from over a century ago, a time when human specialists executed the core mechanism by recording in paper-and-pencil order books the bids and offers handed to them by floor traders. Modern electronic markets have replaced human specialists with ultra fast computers, but the core mechanism remains a basic CDA. Advanced traders utilize computers in sophisticated ways, but they do so only on the periphery of the core mechanism (Phase 1.5).[n]
The “continuous” in “continuous double auction” means that bids and offers are sorted by price-time priority and orders are processed serially in continuous time. Serial processing of orders in continuous time creates an advantage for traders with fast response times, who can trade against “stale” orders before slower traders. In other words, fast traders can exploit mechanical or latency arbitrage opportunities.[n] In contrast, batch auctions process orders in batch in discrete time, so there is no speed advantage; orders from fast traders and slow traders alike are executed simultaneously at a uniform clearing price, improving welfare and reducing transaction costs.[n]
CDAs are used as a financial "uber-hammer" for the trading of multiple related securities, such as options in an option chain. Each security trades separately on an independent order book, which fragments liquidity and segregates prices. Fragmented liquidity exacerbates the thin market problem. Segregated pricing of related securities leads to statistical arbitrage opportunities, which, like mechanical arbitrage opportunities, are exploited by advanced traders on the periphery of the core mechanism (Phase 1.5).
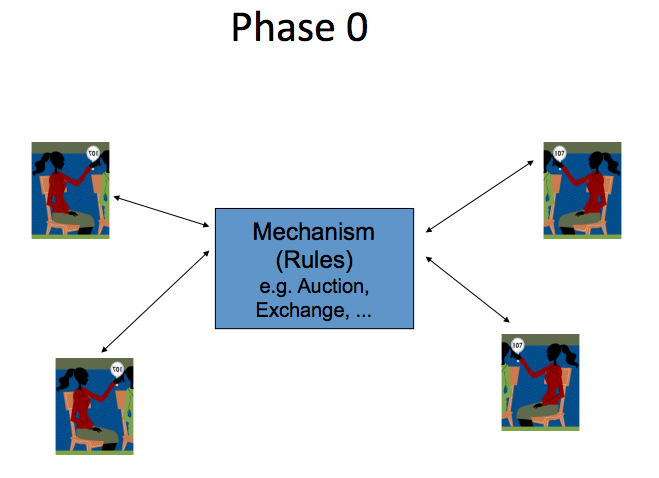 Phase 0: Human operated mechanism. (source: [N])
Phase 0: Human operated mechanism. (source: [N])
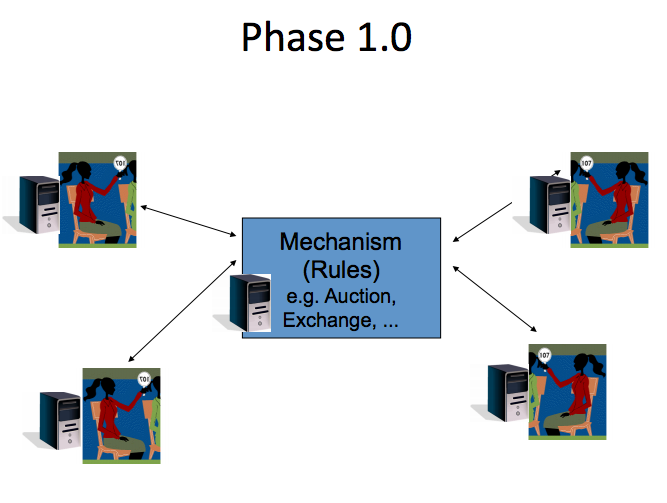 Phase 1.0: Computers mimic humans; mechanism is faster but not better. (source: [N])
Phase 1.0: Computers mimic humans; mechanism is faster but not better. (source: [N])
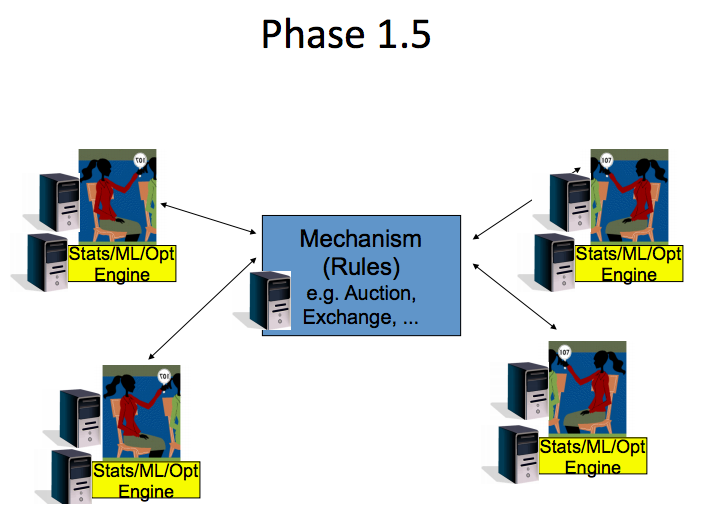 Phase 1.5: Agents on the periphery get smarter, but the core mechanism is still dumb. Computational power on the periphery identifies abundant arbitrage opportunities in the center. (source: [N])
Phase 1.5: Agents on the periphery get smarter, but the core mechanism is still dumb. Computational power on the periphery identifies abundant arbitrage opportunities in the center. (source: [N])
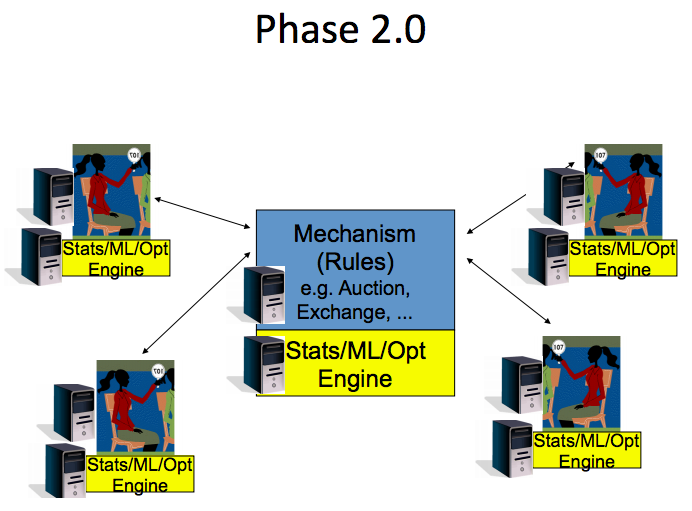 Phase 2.0: Smart core mechanism does basic statistical inference, automatically propagating price changes and thus eliminating opportunities for arbitrage. Agents on the periphery are rewarded for providing predictive information rather than for correcting short-term mispricings. (source: [N])
Phase 2.0: Smart core mechanism does basic statistical inference, automatically propagating price changes and thus eliminating opportunities for arbitrage. Agents on the periphery are rewarded for providing predictive information rather than for correcting short-term mispricings. (source: [N])
Smart markets replace multiple double auctions with a sophisticated combinatorial auction as the core mechanism (Phase 2.0).[n] Because double auctions simply sort bids and asks, they are only capable of bilateral order matching on two-sided order books. And since double auctions can only do bilateral order matching, multiple securities must be traded in parallel on disconnected, two-sided order books; an arrangement that fragments liquidity. In contrast, combinatorial auctions solve complex optimization problems, so they can perform multilateral order matching on a united, multi-sided, combinatorial order book. Since multilateral order matching on a combinatorial order book enables multiple securities to be traded together in the same combinatorial auction, smart markets aggregate liquidity.
Furthermore, a combinatorial mechanism can integrate the prices of related securities, ensuring that prices remain arbitrage-free even if unsophisticated traders place mispriced orders. That is, the core mechanism itself maintains arbitrage-freeness by propagating price changes automatically. In contrast, the conventional method of using CDAs relies on advanced traders to maintain arbitrage-freeness by exploiting mispriced orders (Phase 1.5). Thus, by automatically integrating prices and aggregating liquidity, smart markets improve the welfare of the average trader and reduce their transaction costs, resulting in a more efficient market.[n]
0.1 Stablecoins and market liquidity
Mechanisms designed to create stable-value cryptoassets, or "stable-coins", can be categorized as two basic types: (1) monetary policy schemes, and (2) hedging strategies. Monetary policy schemes attempt to stabilize price by adjusting coin supply;[n] whereas hedging strategies stabilize value by transferring price volatility risk from the hedgers to speculators. On the one hand, monetary policy schemes are only effective during expansion, or periods of increasing demand, and don't work during periods of contraction ("pushing on a string"). On the other hand, hedging strategies are only usable when liquidity is available, as every hedger must be matched with a speculator.
Both types of stablecoin mechanisms ultimately depend on market liquidity, though for hedging strategies the dependency is more explicit. If we assume that liquidity will always be available, then in theory many different schemes and strategies could work. But in practice, without sufficient liquidity any mechanism will fail or cease to be usable due to wide spreads and high transaction costs.
Note that there are multiple types of liquidity, such as “funding liquidity” and “balance sheet liquidity”, and the term “liquidity” is often used ambiguously. We use it only in the strict sense of market liquidity, or bid-ask spread and order book depth. The other types of liquidity and their relationships to monetary policy, price stability, and solvency will be discussed in the long version of this document. For now, a quick-and-dirty comparison between monetary policy and hedging strategies is included in the appendix. But since both stablecoin types ultimately depend on market liquidity, it is our primary concern.
The specifics of market liquidity and trading mechanisms are studied in the field of market microstructure, a topic that is not typically covered in microeconomics and macroeconomics courses. Most economics students are taught to abstract away from particular trading mechanisms and study general models of supply and demand equilibrium under the assumption of perfect liquidity.[*]
The approach in this document is to avoid making any assumptions about market liquidity. To that end, the focus necessarily turns to market structure and design. In particular, we discuss how a combinatorial market structure enhances liquidity for hedging strategies, the benefits of batch auctions with uniform-price clearing, and how automated market makers can be used as reliable default liquidity providers.
Relevant topics that we do not discuss include: querying external price feeds and resolving market outcomes (e.g. Truthcoin voter consensus, SchellingCoin data feeds, or semi-trusted oracles and oracle services), and smart contract implementation details (e.g. bitcoin sidechains, Ethereum scripts, or various "decentralized ledger" platforms); there is much discussion about these topics elsewhere.
0.2 Four essential market mechanisms
In any healthy market, we find four essential mechanisms: (1) an issuer, (2) a clearinghouse, (3) an auctioneer, and (4) a market maker. Cryptocurrency markets can be analyzed in terms of whether or not these four mechanisms are on-chain mechanisms or third-party agents. Bitcoin has an on-chain issuer (the block reward) and an on-chain clearinghouse (a public-private key protocol that transfers coins from input addresses to output addresses). But the auctioneers and market makers for bitcoin are third-party agents, usually on centralized exchanges. Ripple has an on-chain clearinghouse and on-chain auctioneers (or "on-ledger"), as order book and trade matching functionality is implemented directly in the protocol. But the issuers and market makers on Ripple are third party agents. Truthcoin proposed on-chain market makers. On-chain mechanisms disintermediate by replacing middle-men who have conflicting incentives with decentralized autonomous agents obligated (by cryptographic verification) to execute common computer code on a peer-2-peer network.
Issuers and clearinghouses will be discussed in the long version of this document. For this quick-and-dirty version, we focus on auctioneers and market makers.
A market maker is a temporal intermediary between buyers and sellers who demand immediacy but arrive at different times. All market makers must have funds and must take risk as they are direct participants in the market, using their own funds to buy from sellers and sell to buyers. By staying in a market across time and continually acting as a counterparty in trades, the market maker is said to provide liquidity to the other buyers and sellers as they come and go. In the financial industry, market makers have also been called specialists, stockjobbers, dealers, broker-dealers, flow traders, and scalpers.
An auctioneer is an agent who conducts an auction, responsible for organizing buyers and sellers (traders) arriving at the same place. Auctioneers don't have funds and never take risk as they are mere organizers, not participants. Auctions that require all participating traders to transact at the same time are batch auctions (also known as call auctions). Auctions that permit traders to transact whenever they arrive, or in other words at different times, are continuous auctions.
In order for trade to occur, traders must meet at the same place and time. If traders don't meet, then they can't trade (the most basic form of market failure). Auctioneers enable trade by bringing traders together to the same place (and for batch auctions, at the same time as well). Market makers enable trade by intermediating between traders who come to the same place but at different times. Arbitrageurs enable trade by intermediating between traders who are in different places. In modern electronic markets the auctioneers are order matching algorithms, and the places where traders meet are Limit Order Books.
1 Combinatorial Bundles/Portfolios
In a traditional auction such as an english auction or a dutch auction, one seller sells a specific amount of a single item to multiple potential buyers (the bidders). In a double auction, there are multiple sellers and multiple buyers, both sides offering to sell and offering to buy various amounts of a single item. For over a century, the double auction has been the standard mechanism most commonly used for the trading and exchange of financial instruments (i.e. stocks, bonds, currencies, futures, options, and so on).
In a combinatorial auction, multiple buyers bid on combinations of various amounts of multiple items referred to as bundles, packages or portfolios. Examples of items commonly traded in combinatorial auctions include wireless spectrum licenses, bus routes, and personal property sold in estate auctions. Rossenti et. al., who first proposed combinatorial auctions, described them as smart markets.[n] The term smart market emphasizes that combinatorial auctions solve complex optimization problems; in contrast, legacy auctions execute simple sorting processes.
1.1 Binary options and portfolio payoffs
The example market that this document presents is a combinatorial auction where the items traded are binary options. Generically, the payoff of a binary option is either zero, or greater than zero. But our market trades a specific class of binary options where the payoff is either zero or one (a unit amount of a numeraire), depending on the future state of the "world", or outcome of the event. In an ideal model of a market, or a complete market, binary options are available for all possible states. Such binary options are called Arrow-Debreu securities. They are also called, with varying degrees of accuracy: Arrow securities, state-price securities, pure securities, primitive securities, contingent claims, state-contingent claims, state claims, time-state claims, atomic securities, atomic time-state claims, and atomic claims.[n] When issued by a cost-function based Automated Market Maker (AMM), they are just called "shares" (as in, shares of a specific outcome). We will forego technical accuracy and generally use the terms binary option and atomic security.
Binary options are simply bets (or wagers) on some event where losing bettors receive nothing, and winning bettors receive a unit amount of some currency. The chosen currency is called the numeraire (e.g. dollars, yuan, euros, bitcoins or what have you), and the unit amount is defined arbitrarily (e.g. $0.05, $1, $20, or $300). The event results on which bets can be placed are called "states of the world", or the outcome space. For example, if a week into the future the Kansas City Chiefs will play against the Green Bay Packers in a Super Bowl game, and spectators bet on which team will win, they can be viewed as trading two different binary options in a market with two states-of-the-world (in other words, two mutually exclusive outcomes, or two "disjoint and exhaustive" outcomes).
The amount paid to place such a bet, or the cost to purchase the binary option, is called the state price. Whereas traditional bets cannot be resold, option contracts are traded in a market, therefore state prices can fluctuate as long as the market is open. If the sum of the state prices is less than 1.0, then a buyer can purchase an option for each state and be guaranteed to earn a profit. When state prices sum to 1.0, the market is arbitrage-free. When the sum is greater than 1.0, the additional amount over 1.0 is the overround, or the spread between bids and asks. The overround constitutes the market maker’s commission. State prices represent betting odds, or the aggregate estimated chance of each outcome being realized in the future. In mathematical terms, state prices represent a probability distribution over an outcome space.
In our example market, the outcome space is the price of a volatile cryptocurrency (BTC) at a future expiration date. (Or more precisely, the outcome space is the set of possible future prices, one of which will be realized on the expiration date.)
Since our example market is combinatorial, traders buy and sell contract bundles, or portfolios of atomic securities, or equivalently bundles of binary options. Such bundles or portfolios could be described with many different names that would all be roughly equivalent, such as: "packages of time-state claims", or "linear combinations of primitive securities", and so on. We will use the terms bundle and portfolio interchangeably. We use bundle to emphasize that they are traded in a combinatorial auction, and portfolio to emphasize that they are financial securities.
Each portfolio is a specification of a payoff vector. Each component of a portfolio specifies the quantity of binary options on a particular outcome, and is equal to the portfolio's payoff in that state. Each binary option in a portfolio is an atomic security. An atomic security is a unit vector of a vector space called the payoff space. The number of atomic securities is equal to the dimensionality of the payoff space. Every possible portfolio in a market is a linear combination of its atomic securities. In other words, each portfolio is a point in the payoff space, and the payoff space is spanned by the atomic securities. A portfolio that has the same payoff in every state is called a riskless security.[n]
1.2 Synthetic positions with portfolios of binary options
The interactive chart below provides a visualization of how portfolios of binary options can replicate the cash flows of conventional options and conventional futures. A trader who buys such a portfolio will have a synthetic position with a payoff that replicates the payoff of the conventional financial instrument. Since options and futures are derivatives, our example market should be compared to markets for derivatives rather than spot markets.
The outcome space of our market is not continuous, but a set of discrete prices, so conventional payoffs are only approximately replicated (a continuous price space is mapped to a set of discrete intervals, and each interval is approximated by a single discrete price). In the example below, the set of fifteen discrete prices is [$5.13, $5.64, ... $17.72, $19.49], roughly the range from $5.00 to $20.00. These prices were chosen for their logarithmic distribution, which results in a more intuitive bar chart. The range was chosen to center on a $10.00 starting price, and with a lower bound of ~$5.00 so that a 50% price decrease could be hedged. The upper bound of ~$20.00 is symmetric with the lower bound.
Since the outcome space in this example is a set of fifteen discrete prices, it is a market with fifteen dimensions spanned by fifteen binary options. A portfolio or bundle is therefore a vector with fifteen components. Bundles are combined by adding their vectors. Bundles that combine to form a riskless security are called complementary bundles or matching bundles; and the riskless security is called a complete bundle or exhaustive bundle. Because bundles are matched multilaterally in a combinatorial auction, a complementary or matching set can contain more than two bundles.
Since complete bundles are riskless securities, by matching complementary bundles into complete bundles the auctioneer ensures that the funds paid in will be equal to the funds paid out, regardless of which outcome is realized on the expiration date. In other words, by taking the bundles that traders buy individually and combining them to form complete bundles, the combinatorial auctioneer maintains a "balanced book" or "matched book" (except while bookies and dealers charge an overround or a spread, our auctioneer does not charge a spread).
If traders wish to buy a set of bundles that can't be matched into a complete bundle, then an automated market maker is needed. An automated market maker provides liquidity in the form of a bundle which is complementary to an incomplete set. In other words, the market maker sells a complementary bundle, which the auctioneer then combines with the traders' bundles to form a complete bundle. Any time the market maker sells a complementary bundle, the state prices will change in accordance with the market maker's cost function. In contrast, an auctioneer can match bundles without necessarily changing the state prices (this can be viewed as equivalent to buying a complete bundle from a market maker, since the state prices do not change when a market maker sells a complete bundle).
Note that this first chart is only a visualization of bundle payoffs, not auctioneer and market maker activity. The auctioneer and the market maker are the focus of the second and third charts; we mention them here only to point out their roles in matching bundles and forming complete bundles.
Notes for reading and using the chart:
- In the bets section, pairs of matching bundles are indicated by an arrow symbol .
- More than two bundles can also match each other. For example, "Straddle", "Write a Call", and "Write a Put" combine to form a complete bundle, as do "Butterfly", "Buy a Put", and "Buy a Call".
- When matching bundles are plotted in “Stacked” mode and the y-axis is plotted in BTC, the bar chart has the particular appearance of being flat across the top.
- The bundle sizes are fixed.
- For option bets, the sizes are fixed at one contract unit (approximately), and the call option sizes are scaled to be symmetric with the put option sizes.
- For CFD bets, the sizes are fixed so that both the long and the short bets risk 100 BTC ($1,000 at $10 BTC/USD price).
- The stable portfolio has the same payoff in USD value for every outcome. We can say that the stable portfolio is a riskless security in USD-space. The stable portfolio is the "Short Bundle" at 0x leverage, and it matches the "Long Bundle" at 2x leverage.
Since this example is an on-chain market, our choice of numeraire is restricted to a native cryptocurrency (BTC). This restriction of the numeraire makes it challenging to replicate the payoffs of conventional instruments, which are traded in markets that use USD as the numeraire. To observe how the numeraire restriction limits our ability to construct payoffs, use the y-axis toggle switch to convert the "Payoff Amount" scale between BTC and USD. Note that the y-axis toggle only converts the payoff denomination, which should not be confused with the market numeraire. The numeraire remains BTC and cannot be changed.
Notice that component payoffs of complete bundles are balanced when measured in BTC, but lopsided when measured in USD (the bars on the right-hand side of the bar chart are taller than the bars on the left). The lopsidedness of payoffs measured in USD is a consequence of using BTC as the numeraire. One way to overcome this is to take the synthetic-USD (i.e. the "stable portfolio") created in this BTC-numeraire market, and use it to create a second market with synthetic-USD as the numeraire. Another option is to utilize a USD asset from a third-party issuer; we excluded that option here because for a wholly on-chain "stablecoin" all four essential market mechanisms must be on-chain.
The leverage of these synthetic positions is based on the combinatorial market structure, that is, combinations of binary options. Each binary option in the portfolio is a derivatives contract on a specific outcome, i.e. a particular future spot price. Thus, these portfolios specify contracts at multiple price levels, similar to a strategy described before as "Stabilizing Forwards".[n]
There is an important difference between these synthetic positions and conventional leverage instruments like futures and (American or European-style) options. While binary options have bounded payoffs and bounded losses (or fixed-returns and fixed-losses), conventional leverage instruments have unbounded payoffs and/or unbounded losses. The long version of this document will contain further discussion of conventional leverage mechanisms, including equity margin, future margin, and forex. But in brief, the unbounded payoffs and losses of conventional derivatives are supported by a hierarchical arrangement of credit and liability, with a central counterparty at the top, member brokers in the middle, and customers at the bottom. The central counterparty is liable if a member broker defaults; and member brokers are held liable if their customers default (i.e. if a customer cannot cover a margin call). Additionally, to reduce the risk of defaults, the exchange sets lock limits that restrict the trading of less liquid contracts to within a permitted price range, which is adjusted daily when the market re-opens. Without such limits to restrict price volatility, hierarchies of credit and liability experience brittle failure modes triggered when market liquidity momentarily vanishes, leaving stop-loss orders unexecuted due to massive slippage. In contrast, a market structure based on binary options does not have such systemic risks because payoffs and losses are bounded.
In the chart above, users can select several types of bundles and visualize the component payoffs. However, users cannot change the bundle quantities, nor enter limit prices to bid on bundles, as they would in a user interface for an order book. Thus, the chart above is a visualization of portfolio payoffs, and not a visualization of an order book interface where users trade portfolios with bundle bids. A combinatorial order book for trading portfolios as bundles is presented in the next example.
1.3 Related work
The combinatorial market described in this document is not novel. As presented here, the market mechanism is most similar to three predecessors: (1) “combined-value trading” by Bossaerts et. al, who describe their mechanism as an “intermittent call market with a single electronic open book” wherein investors “submit orders for packages of securities and the system matches trades and computes prices by optimally combining portfolio orders”;[n] (2) Lange & Economides, who describe a "Pari-mutuel Derivative Call Auction" (PDCA) as a “game conducted as a call auction” with a “parimutuel microstructure with notional claims, limit orders, and ‘claim bundling’ across states”;[n] and (3) Peters et. al. who, building on Lange & Economides, call their mechanism a “convex parimutuel call auction mechanism” (CPCAM).[n]
All three mechanisms are combinatorial in nature. To emphasize this, we use the generic term “combinatorial auction” in this document. All three mechanisms are also based on call auctions, otherwise known as batch auctions. The term “call auction” (or call market) describes a double auction with batch order processing and uniform-price clearing. We use the term “batch auction” instead, following Budish et. al. who call their (non-combinatorial) mechanism “frequent batch auctions”, which they describe as "uniform price double auctions conducted, e.g., every tenth of a second." Since the mechanism we describe is, like the three predecessors, both a combinatorial auction and a batch auction, we thus use the term “batch combinatorial auction”. We find “batch combinatorial auction” preferable as it is easily contrasted with the standard “continuous double auction”, and in combination with “combinatorial order book”, the primary features are emphasized.
Also relevant is a fourth predecessor, Yoopick by Goel et. al., who describe it as a "combinatorial sports prediction market that implements a flexible betting language, and in turn facilitates fine-grained probabilistic estimation of outcomes."[n] Yoopick defines a market structure where the outcome space is the point spread between the final scores of two teams in a sports game, such as an NFL football game. In comparison, recall our example market for a Super Bowl game, where we structured the outcome space into two mutually exclusive outcomes: either the Chiefs win, or the Packers win. A market structure over the point spread has more than two outcomes, for example: [.., -3, -2, -1, 0, +1, +2, +3, ...], where the set of positive numbers +x is assigned to represent the Packers winning by x points, and the range is bounded on both sides at some arbitrary cutoff. To bet on a tie, participants buy binary options on "0"; to bet on the Packers winning by three or more, participants buy the bundle of binary options [+3, +4, +5, ...]; and so on. With this market structure, bettors can purchase bundles that replicate the payoffs of conventional sportsbook bets, such as money line bets and point spread bets; or they can purchase custom bundles with exotic payoffs.
While Yoopick defines a combinatorial market structure on the final point spread of a sports game, we define a combinatorial market structure on the future spot price of a digital currency (i.e. the BTC/USD spot price on the expiration date). Thus, the market structure that Yoopick defines for betting on sports is very similar to the market structure that we define for trading digital currency derivatives. But the respective mechanisms have a fundamental difference: while Yoopick uses a combinatorial market maker (LMSR) to accept bets, we use a combinatorial auctioneer to match orders. That is, Yoopick uses a cominatorial market maker in a quote-driven mechanism that is only capable of accepting market orders because it does not have an order book. Whereas we (like our first three predecessors) use a combinatorial auctioneer in an order-driven mechanism that is capable of matching limit orders on a combinatorial order book. To put it another way, Yoopick uses LMSR to accept combinatorial market orders at discriminatory clearing prices determined by serial processing in continuous-time. In contrast, we use an LP algorithm to match combinatorial limit orders at uniform clearing prices calculated by batch processing in discrete-time.
Recall that we identified four essential market mechanisms: an issuer, a clearinghouse, an auctioneer, and a market maker. The difference between Yoopick, which only utilizes a combinatorial market maker, and the first three predecessors, which all utilize a combinatorial auctioneer, highlights the distinction between auctioneers and market makers. In the context of an order-driven market, the auctioneer processes limit orders and market orders as they arrive at the order book; while market makers generate limit orders and send them to the order book. The next two examples focus on these two essential market mechanisms, respectively.
2 Combinatorial Auctioneers
In the next example, we experiment with using a combinatorial auctioneer to match limit orders to buy bundles, or combinatorial bids. While a conventional bid in a double auction imposes a price constraint on a single item or dimension, a combinatorial bid (or bundle bid) imposes a price constraint on multiple items or dimensions. A combinatorial auctioneer sums, or integrates, the set of state prices under the constraints imposed by bid limit prices and component quantities, and matches bids when limit prices cross.
In our example market, each state price is the price of a binary option. The combinatorial auctioneer ensures that the sum of the state prices is never less than 1.0, so there is never a combination of binary options that can be purchased for a guaranteed profit. In other words, the odds are always coherent, because the combinatorial auctioneer ensures that the market is always arbitrage-free. Or to put it another way, since binary options are derivatives, the combinatorial auctioneer enforces the law of one price in the market’s valuation of the underlying security. In our case, the underlying security is a digital currency (BTC).
Note that combinatorial auctions are a special case of the more general class of combinatorial exchange mechanisms. In a combinatorial exchange, there are multiple buyers and multiple sellers. In a combinatorial auction, there is only a single seller. Our example combinatorial market is a combinatorial auction, where the auctioneer also acts as the single seller, and the items sold are derivative contracts. Thus, when two traders enter into a contract, with one taking the short position and the other taking the matching long position, they are both "buying" distinct contracts from the auctioneer, who holds the funds or collateral until payout when the contract expires. This aspect of our combinatorial auction, where short positions are opened by "buying", is discussed further in section 2.4 with a comparison to conventional markets where short positions are opened by selling.
2.1 Batch Combinatorial Auctions vs Continuous Double Auctions
The standard method of trading derivatives uses multiple double auctions. Each derivative trades on an independent order book, even if the derivatives are related in value. For example, options for the same security (i.e. options in the same option chain) are logically related; premiums for different strike prices are correlated. But since a double auction is only capable of bilateral matching of bids and asks for a single item, each strike price in the chain is traded on a separate order book. That is, different strike prices are traded in parallel on disconnected order books, as if their values were unrelated. Thus, the standard method of using double auctions is a mechanism in which related items are traded in different places, fragmenting liquidity and segregating prices. Fragmented liquidity increases transaction costs and segregated prices create arbitrage opportunities, resulting in reduced market efficiency.
In contrast, a combinatorial auction is capable of multilateral matching between multiple limit orders for multiple items in a combinatorial order book. To put it another way, a combinatorial auction aggregates limit orders for related items into a unified liquidity pool. Thus, a combinatorial auction enables related items to trade in the same place, aggregating liquidity and integrating prices. Aggregated liquidity reduces transaction costs and integrated prices eliminate arbitrage opportunities, resulting in improved market efficiency.
Double auctions are distinguished as either continuous auctions, or batch auctions. Batch auctions, also known as call auctions or discrete-time auctions, process orders in batch in discrete-time. In contrast, continuous auctions process orders serially in continuous-time. Serial order processing in continuous-time inherently uses a discriminatory pricing rule (also called pay-as-bid pricing), meaning that different trades transact at different clearing prices. Batch auctions are generally defined by the use of a uniform pricing rule (also called single-price clearing), meaning that all trades executed in the same batch transact at the same clearing price. Call auctions, batch auctions, discrete-time auctions, (also "uniform price auctions" and "clearing price auctions"), are all terms used to describe auctions that use a uniform pricing rule, or uniform-price clearing. In this document, we use the term "batch auction" because it emphasizes that orders are processed in batches; and we use "uniform-price clearing" because it emphasizes that trades executed in a batch all transact at the same clearing price.
Combinatorial auctions generally match orders in batch, though they may or may not use uniform-price clearing (for example, combinatorial auctions that maximize the auctioneer's revenue do not use uniform-price clearing). The combinatorial auction that we present matches orders in batch and uses uniform-price clearing. To make the batch processing feature explicit and emphasize the distinction from a continuous double auction, we use the term batch combinatorial auction.
Serial order matching or processing is a procedure that matches incoming orders according to time priority. Time priority and discriminatory price clearing are inherent to serial processing in continuous time, creating perverse incentives for an investment arms race for tiny speed improvements. Such speed improvements result in a market that is more efficient in time space but less efficient in volume space. That is, the market price may be updated sooner, but counterintuitively, more volume is transacted at stale prices. In contrast, frequent batch auctions with uniform-price clearing prioritize volume-efficiency over time-efficiency.[n] With batch processing in discrete time, clearing prices may not be updated instantly, but more volume is transacted at correct (i.e. not stale) prices. The improved volume-efficiency of batch processing results in increased welfare for the average trader. Additionally, since market makers are temporal intermediaries, processing all transactions simultaneously in batch auctions reduces intermediation by market makers.
Put another way, in continuous-time markets liquidity is "necessarily fragmented temporally".[n] And in markets with multiple double auctions, liquidity is fragmented spatially, or in different places (i.e. on different order books). Hence, with multiple continuous double auctions, liquidity is fragmented both spatially and temporally, or in different places and different times.
Thus, batch combinatorial auctions provide two distinct benefits over continuous double auctions. First, the combinatorial matching brings traders of related items together to the same place; related items trade on the same combinatorial order book rather than on separate order books. Second, the batch processing brings traders together at the same time; different traders transact simultaneously at the same uniform clearing price, rather than at different prices determined by trivially tiny differences in their arrival times. In short, batch combinatorial auctions aggregate liquidity by bringing traders together at the same place and time.
2.2 Batch processing and mechanical arbitrage
To be clear, when we say that a combinatorial auction is arbitrage-free because it integrates prices, we mean arbitrage-free in a local sense. That is, the integration of prices removes "statistical arbitrage" opportunities between related items on the same combinatorial order book. On conventional order books, these "StatArb" opportunities arise because disconnected double auctions do not integrate prices. Advanced traders watch for these opportunities to arise, using strategies such as pairs trading or portfolio cointegration. Such StatArb strategies can take advantage of short-term mispricings that occur between different items on the same exchange, in other words local arbitrage opportunities.
StatArb is distinct from arbitrage of a different type, which takes advantage of different prices for the same item on different exchanges. This type is arbitrage in a global sense. Exploiting these global opportunities does not require any form of statistical valuation, just a difference in price for the same item, hence the term "mechanical arbitrage". With continuous-time order processing, these mechanical arbitrage opportunities are exploited by the fastest traders, so the term "latency arbitrage" is also used.
While combinatorial order matching eliminates local statistical arbitrage opportunities, there may of course still be global arbitrage opportunities between the local combinatorial market and some external market. This is where batch processing comes in: batch processing with uniform-price clearing eliminates mechanical arbitrage opportunities. To be clear, if only the local market utilizes batch processing with uniform-price clearing, and the external market utilizes conventional serial processing and discriminatory pricing, then there will still be arbitrage opportunities in the external market. That is, the fastest traders can still profit by propagating prices from the local market outward to the external market. But arbitrage opportunities in the other direction, from the external market into the local market, are eliminated.
To understand why mechanical arbitrage opportunities from external markets into the local market are eliminated, consider how mechanical arbitrage works in a continuous-time market. With the discriminatory pricing inherent to continuous-time serial order processing, the fastest trader arrives first and gets the best price by "sniping" stale limit orders before slower traders can cancel them. But with batch processing and uniform-price clearing, the orders of fast and slow traders alike are processed simultaneously; a stale limit order does not get sniped by the fastest trader. Furthermore, when a stale limit order left over from a previous batch period is matched in the new batch period, it does not get matched at the stale limit price, but at the new uniform clearing price.
Since in each batch period multiple traders arrive with new bids, the uniform clearing price is updated every period to reflect the most recent prices on external markets. But mechanical arbitrage is eliminated because all orders transact simultaneously at the uniform clearing price, not at stale limit prices. All traders transacting in the batch period get the same fair price, regardless of whether they used a limit order or a market order.
In the context of decentralized exchanges and order matching on a blockchain, the terms "call auction" or "batch execution" are sometimes used to describe an order matching mechanism that uses discriminatory pricing.[n] This usage creates confusion because call auctions or discrete-time batch auctions are generally understood to use uniform-price clearing. As noted by Parsons, "Indeed Madhavan distinguishes continuous and discrete-time auctions precisely by the fact that continuous auctions use discriminatory-pricing and discrete-time auctions use uniform-pricing."[n]
Whether orders are processed serially in continuous-time or executed in batch in discrete-time, discriminatory ("you get what you asked for") pricing is inherently problematic. O'Hara (speaking about a model in Rock [1991], "The Specialist's Order Book") explains the "adverse selection problem facing traders who submit limit orders":[n]
The problem is that as orders execute, market participants update their beliefs on the asset's true value. Following a large sell order, the market maker lowers his expectation of the asset's value to reflect the risk that large orders are more likely the result of information-based trading. This can cause his quoted price for a large sale to fall below that of orders on the book, thereby allowing the limit orders rather than the market maker to clear the trade. Since the limit orders then transact at a price above the asset's new expected value, the limit order trader has an expected loss on the trade. Indeed, given this adverse selection problem, the optimal strategy for a limit order trader is not to trade at all, and the book would simply not exist. (O'Hara, 1995, p.193)
At the root of this problem is the "free option" property of limit orders matched with pay-as-bid, discriminatory pricing. In an analysis by Beiner & Schwartz, a trader who posts a limit order can be viewed as an option writer who receives a payoff that differs depending on whether an informational event occurs or a liquidity event occurs (i.e. whether a news announcement causes a price change, or the market impact of a market order causes a momentary dip). Posting a limit order is equivalent to writing a "free option" for anyone to take, and "the payoff the investor receives from a liquidity event is the compensation (s)he obtains from a 'free' option to other participants." Beiner & Schwartz conclude that in continuous-time auctions, limit orders have fixed or bounded payoffs ("payoff of a binary option"); whereas in discrete-time call auctions, limit orders have unbounded payoffs ("payoff of a standard option"). Thus, "introducing a call auction implicitly introduces a new financial asset for investors."[n]
Consider a trader, Alice, who posts a limit order to buy, and take two example events. One is a liquidity event: a large market sell order temporarily pushes the price below the mid-price. The other is an informational event: a large seller, Bob, dumps a market sell order right as bad news is announced, so the price falls and does not bounce back. In a continuous-time market, how does Alice fare under each event? In the case of the liquidity event, she wins a fixed payoff: the difference between her limit price and the mid-price. In the bad news case, she loses, and she receives no compensation from Bob when he takes her option for free and exercises it. In other words, Bob snipes her limit order, and she loses to him the the difference between her limit price and the new lower price.
How does Alice fare in a discrete-time batch market? In the liquidity event, she wins the difference between the uniform clearing price and the mid-price. So her payoff is not fixed by her limit price; instead, it varies with the uniform clearing price. In the bad news event, she loses, but not as severely as in the continuous-time market because she only pays the uniform clearing price, not her limit price. Thus, she receives compensation from Bob in the form of a premium equal to difference between her limit price and the uniform clearing price.
So, in a continuous-time auction, limit orders are free options available on a first-come-first-serve basis, exercisable at the limit price. In contrast, limit orders in a discrete-time batch auction are not free options; rather, they are orders which specify a reserve price. That is, a limit order in a batch auction is an order to transact at any price better than the reserve price. Even if a buyer is careless in specifying their reserve price, they will still only pay the fair, uniform clearing price.
On top of being an unfair mechanism for average traders (who aren't informed and don't demand microsecond immediacy), the discriminatory pricing implicit in continuous-time auctions also makes it difficult for market makers to provide liquidity. In modern HFT parlance, discriminatory pricing enables fast traders to "snipe" limit orders, whether those limit orders are posted by market makers or average traders. In floor trader parlance, those with a speed advantage can "pick off" dealer quotes:
This highlights what has commonly been termed the "free option" property of limit orders. Because the limit order trader precommits to buying or selling at a particular price, he or she has in effect written an option at the specified strike price. As market prices change, this option can move in or out of the money, exposing the writer to the risk of the option being exercised at his expense. Stoll [1990] gives an example of this occurring in the Intermarket Trading System. With ITS, a dealer in Cincinnati can post quotes in an NYSE-listed stock that will automatically execute. If a floor trader in New York sees a large block in the stock or learns of any other event that might lower the price on the NYSE, he can send a sell order to Cincinnati and "pick off" the dealer before he has a chance to change his quote. (O'Hara, 1995, p.197)
With discriminatory pricing in continuous-time, the speed at which one can post and and cancel orders is critical. As a result, in order to provide liquidity without suffering adverse selection to the point of bankruptcy, market makers must be as fast as the fastest traders. The costs paid to stay fast are "arbitrage rents", which "harm liquidity provision and induce a never-ending socially-wasteful arms race for speed".[n] These harmful arbitrage rents are inherent to the continuous-time discriminatory-pricing market design.
In the context of order matching on a blockchain, whether serial or "batch", the use of a discriminatory pricing mechanism merely swaps the HFT arms race with a block mining race. Since discriminatory pricing enables the miner of a block to snipe any limit order in that block, anyone who posts a limit order is writing a free option for miners. Liquidity providers, rather than competing on price by posting limit orders at narrower spreads, can instead invest in block mining speed for an advantage in sniping. As explained by Budish et. al., "arbitrage rents lead to a classic prisoner's dilemma". In the case of a proof-of-work blockchain, investing in a faster hash rate is the dominant strategy. Even for consensus mechanisms other than proof-of-work (i.e. any blockchain or distributed ledger), discriminatory pricing is still problematic because snipers can still collect arbitrage rents. If the profit from market making is less than the cost paid in arbitrage rents, which is the case when order flow is insufficient or prices are too volatile (losses from sniping are greater when prices are more volatile), then the optimal strategy is to not post limit orders at all.
Batch processing with uniform-price clearing is a "market design response" that eliminates mechanical arbitrage rents, and thus escapes the prisoner's dilemma. Limit orders can be posted without fear of being sniped, since they transact at the uniform clearing price. And market makers must compete on price rather than speed, resulting in narrower spreads, more efficient markets, and improved trader welfare.[n]
2.3 Matching bundle bids with a combinatorial auctioneer
An order matching algorithm can be seen as a process for solving a system of linear equations. In the case of a continuous double auction, the system has two equations: the best bid and the best ask. The bid and the ask impose constraints (limit price and limit quantity) on two free variables: the clearing price and volume. A clearing price and volume that satisfies the constraints of the bid and the ask is a solution to the linear system. If a solution can be found, then the bid price and the ask price cross, and a trade is matched at the clearing price.
While a double auction matches offers for a single item, a combinatorial auction matches offers for multiple items. Therefore, a combinatorial auction has multiple clearing prices, one for each item. Since the items traded in our combinatorial market are binary options on specific outcomes or states, the clearing prices are called state clearing prices, or state prices. Each combinatorial bid is an equation in a linear system, and each bid imposes constraints on the state clearing prices.
Thus, to match bids in a combinatorial auction, we must find a solution to the linear system using a linear programming (LP) algorithm, or in more modern terminology, a linear optimization algorithm.[n] As an aside, the word "programming" in "linear programming" is incidental for historical reasons. In the field of operations research, where it originated, "programming" was used in the sense of planning and decision-making, rather than "computer programming". In our case, we can think of the combinatorial auctioneer as a decision-maker who uses linear optimization to decide which bids to fill (the "winner determination problem" or matching problem).
Taking this view further, in using an LP algorithm for combinatorial bid matching, the auctioneer solves a dual optimization problem of resource allocation (which bids get filled) and resource valuation (at which state clearing prices). There are several types of solutions to an optimization problem, including: feasible solutions, which are valid under the given constraints but not necessarily optimal; optimal solutions, which are not necessarily unique; and unique optimal solutions. We want unique optimal solutions or, to speak specifically about combinatorial auctions rather than optimization problems in general, unique state clearing prices because otherwise the winner determination decision is arbitrary rather than fair.[n] The LP method we use below will calculate unique state clearing prices if it is given enough bids and the bids are of the right kind (i.e. linearly independent). If it is not given enough bids, then the solution to the system will be underdetermined, and the state clearing prices will not be unique. There are linear optimization methods that ensure a combinatorial auction will calculate unique state clearing prices regardless of the given bids, but they are more complex formulations than the relatively simple LP method we use here.[n] For now, it is instructive to use the relatively simple LP method and better understand the problem we are facing.
2.4 Visualizing a combinatorial order book
Our primary challenge in the example below is visualizing limit orders and state clearing prices in a combinatorial order book. The approach we take is to display an order book for each state. We use an example market of four states, so we display four order books. The difference between our four order books and conventional order books is that conventional order books are displays of (two-sided) double auctions, whereas our four order books display four items trading in bundles through a single (four-sided) combinatorial auction.
To better understand our approach to visualizing a combinatorial order book, first consider a conventional order book for a double auction. The “double” in double auction describes an order book with two sides, bids to buy on one side and asks to sell on the other side. When the best bid has a higher price than the best ask, the two orders are matched and a trade is executed. But which order is the bid and which is the ask is relative to how the order book is displayed. For example, when looking at a BTC/USD order book, a bid is a limit order to buy BTC, and an ask is a limit order to sell BTC. But if the currency pair is flipped to USD/BTC, then a bid is a limit order to sell BTC (buy USD), and an ask is a limit order to buy BTC (sell USD). The order book itself does not actually change. The display using USD/BTC just appears upside-down relative to the conventional BTC/USD.
A combinatorial order book can be understood in the same way. Recall that the items in our market are binary options on future outcomes or states. Returning to the Super Bowl example, there are two possible outcomes and two respective binary options: (1) the Green Bay Packers win, and (2) the Kansas City Chiefs win. A bet that the Packers will win is equivalent to a bet that the Chiefs will lose, and vice versa. Therefore, a bid on the Packers is equivalent to an ask on the Chiefs, and vice versa. Likewise, in a market with three possible outcomes, a bid on the first outcome is equivalent to an ask on the second and third outcomes, a bid on the second is equivalent to an ask on the first and third, and a bid on the third is equivalent to an ask on the first and second.
For larger outcome spaces, the relationship continues to hold: a bid on one outcome corresponds to asks on the other outcomes, and vice versa. We call such corresponding asks phantom asks. The concept of phantom orders has been used before to aggregate liquidity by augmenting conventional order books. Combinatorial bid matching, however, aggregates liquidity inherently with an LP algorithm, so augmenting a combinatorial order book with phantom orders would be redundant. In the chart below, the input to the combinatorial auctioneer (i.e. the LP algorithm) is strictly bids; corresponding phantom asks are only used to help visualize the order book.
In the chart below, bids are plotted as green dots. A bid on a single atomic security (e.g. [0, 1, 0, 0]) appears as a green dot on only one order book, and the corresponding phantom asks appear as orange dots on the other order books. Bids on mixed bundles (e.g. [0.2, 0.3, 0, 0.5]) appear as green dots on multiple order books. Visualizing bids on mixed bundles is difficult because a combinatorial bid’s limit price is a constraint on the whole bundle rather than on individual components, so its not obvious how we should plot them. In the case of an atomic bundle, the bid specifies only one component, so we can use the bid’s limit price to plot the single green dot. But for phantom asks, and components in mixed bundles, it is not clear what prices we should use to plot each component.
For bids on atomic bundles, we plot the bids at the limit price, and we plot the corresponding phantom asks at the complementary price. For example, the three atomic bids [1,0,0,0], [0,1,0,0], and [0,0,1,0], each with a limit price of 0.19, are complementary to a fourth bid on [0,0,0,1] with a limit price of 0.43 (1 - 0.19*3). So the atomic bids at 0.19 have phantom asks at 0.43. For bids on mixed bundles, we use the limit price to plot each component, and we use the state clearing prices to plot the corresponding phantom asks
The LP method we use will only calculate unique state clearing prices if it is given a sufficient set of bids. So to get initial unique state clearing prices, we generate a set of atomic bids (i.e. linearly independent bids) at equal prices. Since there are four states, we generate four atomic bids, all with the same limit price of ¼ = 0.25. To fill in the order book some more, we generate additional sets of atomic bids at equally spaced price levels, resulting in a staircase formation at decreasing price levels (0.25, 0.22, 0.19, …). This generated set of bids represents limit orders placed by a market maker, and is listed under “Market Maker bids” in the chart below.
Also in the chart below is a section for “Trader-entered bids”. Included are three example bids: one bid on an atomic bundle ([1,0,0,0]) and two bids on mixed bundles ([0.4, 0.3, 0.2, 0.1] and [0.1, 0.2, 0.3, 0.4]). The two mixed bundles are complementary to each other, and correspond to the "Short Bundle" and the "Long Bundle" from the previous example, except here we have simplified them down to four dimensions rather than fifteen (the fifteen dimensions in the previous example are the discrete prices between ~$5 and ~$20). All three bundles are normalized, meaning that their components sum to 1.0 (0.4 + 0.3 + 0.2 + 0.1 = 1.0). Normalization makes the limit price of a mixed bundle comparable to the limit price of an atomic bundle. For example, when the limit price of the atomic Trader-entered bid is raised above the initial state price of 0.25, then the Trader-entered bid should match the Market Maker’s bids and get partially filled. And likewise for a mixed bundle; a Trader-entered mixed bundle should also get filled when the limit price is raised above 0.25. Bundles with unnormalized components, however, also have unnormalized limit prices, and so aren’t easily compared.
To be clear, a bundle’s components specify quantities, not prices. For example, a bid for 50 units of the bundle [0.4, 0.3, 0.2, 0.1] is a bid for 0.4*50=20 units of the first component, 0.3*50=15 units of the second component, and so on. Keep in mind that the limit price of the bid is a limit price on the entire bundle, not a limit price on individual components.
Try adjusting the price and quantities of the Trader-entered bids, to see how the system reacts. Notice which bids are filled in full or partially, and how the state clearing prices change in response. Be aware that this example chart is very preliminary; the order books won’t be plotted correctly when too many variations of bundles, prices, and quantities are entered. Ideally, what we want to see is the green bid lines crossing the orange ask lines for bids that are either fully or partially filled. For bids that are fully filled, the green dot should appear below the orange line. For bids that are partially filled, the green dot should appear above the orange line by a vertical distance equal to the remaining unfilled quantity.
Details on the LP calculations can be seen in the javascript console.
Our goal with this example is to gain some visual insight into bundle limit orders on a combinatorial order book, and how the fills and clearing prices are calculated by a batch combinatorial auctioneer. Recall that the LP auctioneer requires a sufficient set of bids in order to calculate unique state prices. Without unique state prices, transacting on a combinatorial order book is a crapshoot, as there is no way to choose one solution of state clearing prices and bid fills over another.[n] In other words, if there is no unique optimal solution, then the “winner determination problem” is underdetermined.
In the example above, a set of staircase bids was generated in order to get initial unique state prices of [0.25, 0.25, 0.25, 0.25]. But the staircase bids aren’t sufficient to get unique state prices after being matched against user-entered bids. The lack of uniqueness can be seen by entering a bid for the portfolio [1, 0, 0, 0] with a limit price of 0.4 and a quantity of 60, resulting in state clearing prices of [0.40, 0.19, 0.22, 0.19]. That the second, third, and fourth components have the state clearing prices [0.19, 0.22, 0.19] is an artifact of the staircase price levels; there is no good reason they aren't instead [0.22, 0.19, 0.19] or [0.19, 0.19, 0.22], as all three are valid optimal solutions to the linear system. Ideally, the combinatorial auctioneer would have calculated a unique optimal solution of [0.40, 0.20, 0.20, 0.20]. But again, guaranteeing a unique optimal solution regardless of the given bids requires a more complex optimization method than the relatively simple method we use here.
The generated staircase “Market Maker bids” in the example above is an ad hoc function for the sole purpose of the visualization. We want to replace it with an automated market maker that could work in practice, such as a cost-function based automated market maker. The next example presents the prototypical cost-function based automated market maker: LMSR.
3 Market Makers
While auctioneers match bids, market makers accept bids. Note the difference between "match bids" and "accept bids": an auctioneer operates an order-driven market by matching the bids that are sent to a limit order book; whereas a market maker operates a quote-driven market (also known as an OTC market) by accepting (or rejecting) the bids that are sent directly to the market maker. However, market makers can also operate in an order-driven market by generating bids and sending them to a limit order book, where they are matched by an auctioneer against the other bids arriving at the order book. The previous example chart presented a combinatorial auctioneer that matches bids. The example chart below presents a combinatorial market maker that generates bids for a combinatorial order book.
Modern market makers are called by various names, including electronic market makers, automated market makers, automated liquidity providers, or more commonly, high-frequency traders. These traders operate market making bots, which are usually presented in the context of a continuous double auction on a limit order book. In literature around prediction markets, a market scoring rule or cost function is employed as an automated market maker, and usually presented as an operator of a quote-driven market. But market scoring rules can in fact be adapted to order-driven markets and viewed as market making bots that post limit orders to an order book.[n][n] In the example below, we present a market scoring rule as a market maker that posts limit orders to a combinatorial order book.
3.1 Liquidity and lemons
While market makers ostensibly perform the service of providing liquidity by posting limit orders, modern HFT market makers also take liquidity with market orders, employing whichever strategy is most profitable on a moment-to-moment basis.[n] Historically, human specialist firms (later called designated market makers) were required by exchange regulations to obey an affirmative obligation to provide liquidity with limit orders when acting as a "principal" (dealer), and to obey a negative obligation forbidding them from taking liquidity with market orders when acting as an "agent" (broker).[n] Unlike the specialists of old who stood inside a trading post executing the core mechanism, market makers in modern electronic markets operate on the periphery of the core mechanism with no such obligations. The inherent conflict between providing liquidity (at a minimal spread) on the one hand, and maximizing profit on the other, is a form of the principal-agent problem and the root cause of "hot-potato" trading and flash crashes in modern electronic markets. Since market makers can (more often than not) predict short-term price drift, they have an information asymmetry over uninformed traders; thus, the limit order book as a market for liquidity is an instance of the classic market for lemons.
Besides the presence of asymmetric information, another property of markets for lemons is a defficiency of effective guarantees/warranties, or in other words, no obligations. Because a smart contract on a blockchain, or blockchain contract (to distinguish from "smart contracts" or oracles operated by third-parties) is obligated by the p2p network to execute the instructions in its source code, they are solutions to the principal-agent problem. Thus, a blockchain contract is a "decentralized autonomous agent" guaranteed to act in the interests of the principal. In our case, the trader is the principal, and the decentralized autonomous market maker (DAMM) is an agent employed as a liquidity provider.
In an essay about the 2007-08 financial crisis, Buiter argues that "liquidity is (or should be) a public good", and that central banks should act as Market Makers of last resort, rather than mere Lenders of last resort. That is, rather than just providing funding liquidity to commercial intermediary banks during market crises, a central bank should add market liquidity to the market directly. A DAMM can be viewed similarly in acting as a market maker of last resort or "dealer of last resort" who directly provides market liquidity. But while a central bank controls monetry policy, a DAMM does not control monetary policy. Consequently, a DAMM must raise funds or "reserve" before it can commit to providing liquidity. Additionally, a central bank is operated by a government-appointed committee, whereas a DAMM utilizes a blockchain as a Coasian solution to negotiate the creation of a common default liquidity provider. In a similar spirit is a proposal by Schwartz, which suggests that a company commit its capital to act as a market maker, buying and selling its own stock in order to stabilize the share price.[n] The proposal explains that the purpose of this corporate "stabilization fund" and market making program is "global demand-smoothing", as opposed to the "local demand-smoothing" obligations of third-party market makers and specialists.
3.2 Market making as a trading strategy
The automated market maker presented below, LMSR, can be viewed as an algorithmic trading program or "trading bot" that executes a market making strategy. The ad hoc function we used in the previous example to generate bids in a staircase formation at a ladder of price levels is also a market making strategy, albeit a simple and naive strategy. Such simple market making bots are theoretically capable of earning a profit under strong assumptions of a mean-reverting price series.[n] But in practice, simple strategies that do not predict short-term price drift suffer adverse selection, bearing losses to other traders in a zero-sum game.[n]
To put it another way, a simple and naive market making strategy is path-dependent, and so might be exploited as a "money pump" until the market maker runs out of funds. In contrast, LMSR and cost-function based automated market makers (AMMs) are path-independent, meaning that the balance of funds and inventory depends only on the state prices, not on the sequence of trades. Path-independence guarantees that the AMM cannot be exploited as a money pump; consequently path-independent AMMs are said to have bounded loss. Note that a profit-charging AMM, such as LS-LMSR, is path-dependent since it uses a cost function that earns a spread. However, path-independence is not necessary to guarantee bounded-loss, it only sufficient. Profit-charging cost functions meet a different requirement, the triangle inequality, which is also sufficient to guarantee the "no money pumps" or bounded loss property.[n]
While the losses of a naive market making bot can be limited by simply limiting its funds, they don't have the "no money pump" bounded loss guarantee, so its funds might run out at any time. Thus, a naive market making strategy cannot be relied on to provide liquidity for as long as a market is open because there's no guarantee that it won't go bankrupt. In contrast, the path-independent (or triangle inequality) bounded loss properties of a cost-function based AMM guarantee that it can stay in the market and continue providing liquidity indefinitely.
Further discussion of the profitability of trading strategies, trading frequency, and bid-ask spreads will be in the long version of this document.
3.3 Combinatorial market makers
Market makers or dealers are usually discussed in the context of a continuous double auction with a two-sided limit order book. But since our market is a combinatorial auction with a multi-sided combinatorial order book, we need a combinatorial market maker. Note that here we use the term “combinatorial market maker” in the sense of “combinatorial bids”, not in the sense of “combinatorial outcomes”. Combinatorial bids describes a market structure with with a tractable number of items (or outcomes, or states), i.e. up to a few hundreds or thousands. Combinatorial outcomes describes a market structure with an intractable or exponential number of outcomes, i.e. in the millions or more. The literature around prediction markets and automated market makers often uses “combinatorial” as shorthand for combinatorial outcomes. Our example market for digital currency derivatives has a structure with combinatorial bids and a tractable, discrete outcome space of fifteen states. Market structures with combinatorial outcomes or continuous outcome spaces is a topic for future work.
The term smart market was originally used to describe combinatorial auction mechanisms because unlike double auctions, which execute simple sorting processes, combinatorial auctions solve complex optimization problems. Combinatorial auctioneers, such as the LP algorithm used in our example, generally solve the "winner determination problem" by matching bids with batch processing in discrete time, so they are batch optimization algorithms. Combinatorial market makers such as LMSR, however, solve a "regret minimization" problem by accepting bids with serial processing in continuous time, and so are online optimization algorithms.[n] Thus, both combinatorial auctioneers and combinatorial market makers solve complex optimization problems; the auctioneer uses a batch algorithm, and the market maker uses an online algorithm. For this reason, combinatorial market makers are also appropriately described as smart market mechanisms.
3.4 Automated market making with a Market Scoring Rule
This example visualizes the Logarithmic Market Scoring Rule (LMSR) as an automated market maker. LMSR, or Hanson's market maker, is the classic original instance of a more general class of cost function market makers. Further discussion of market scoring rules and cost function market makers will be in the long version of this paper.
The aim of this example is to present LMSR as a liquidity provider, by visualizing it as market making bot that places limit orders on a combinatorial order book, and adjusts the prices of its limits orders in response to trading activity. Recall that a market maker must have funds. The initial funds provided to LMSR are the subsidy, so an LMSR market maker is a subsidized market maker. The subsidy amount is set by the B parameter. Try adjusting the B parameter in the example below, and observe how the bid depth on the order book changes.
The components of the inventory vector can also be adjusted, and the state prices will change in response. Changes in market maker inventory are caused by trading activity. Observe that the degree of change in state prices in response to trading activity depends on the B parameter. A larger B parameter represents a market with more liquidity, meaning that more volume can be traded with less price movement.
LMSR and other cost function market makers are usually presented as continous-time trading mechanisms that use serial order processing and discriminatory pricing. But the market we propose uses batch processing with uniform-price clearing. Rather than intermediating in continuous time between buyers and sellers one by one in a serial fashion, a market maker participating in frequent batch auctions intermediates in discrete time across batch auction periods, with between multiple buyers and multiple sellers simultaneously (note that technically, a combinatorial auctioneer intermediates between multiple buyers and a single seller, since it is a combinatorial auction rather than a combinatorial exchange). This role of a market maker has been described before. In the context of call (i.e. batch) auctions, “a market maker could play an important role in animating book building during the precall order entry period."[n] This view sees a market maker as taking "an active role in the book building process" across batch auction periods:
"We see the intermediary as a facilitator who animates the market. The animation process may involve providing capital, not to supply liquidity per se, but to get big buyers and sellers to step forward in a way that enables them to supply liquidity to each other."[n]
This role of a market maker in batch auctions contrasts with the role of a market maker in continuous auctions. In continuous auctions, a market maker provides liquidity directly by placing limit orders, which are then matched by market orders placed by buyers and sellers. So in a continuous auction, buyers and sellers provide liquidity to each other only indirectly, through a market maker acting as an intermediary between each trade.
In contrast, a batch auction enables buyers and sellers to meet directly. The market maker only intermediates between batch auction periods, not between every trade. The role of the market maker is to “animate the order book” with limit orders around the expected clearing price early in the batch period, and to provide price continuity across batch periods. This aligns with the role of an automated market maker in a combinatorial auction where, as we saw, the limit orders provided by the market maker enable the LP algorithm to calculate unique state clearing prices.
4 Future work
An immediate task that remains is to properly integrate a combinatorial order book with an automated market maker (AMM), particularly with batch processing and uniform-price clearing. Some details about discrete-time batch processing that we didn't address include the issue of providing bid-secrecy (i.e. sealed-bids) during each batch period, and determining the optimal batch period length (e.g. seconds, minutes, or longer; or perhaps dynamic periods).[n]
The issue of numeraires is an important direction of research.[n] This issue is especially relevant to on-chain markets where the native numeraire is a cryptocurrency, and it cannot be assumed that a standard numeraire (e.g. USD or EUR) is available.
Future work on combinatorial portfolios includes exploring different ways of defining the market structure or outcome space. For instance, while our example market defined the outcome space on a single expiration date, we could instead define an outcome space over multiple expiration dates. With an outcome space over multiple expiration dates, traders could get even greater leverage or expressiveness with portfolios that specify the path of the spot price over time.
Related to choosing the structure of the outcome space is the use of automated market makers with more advanced cost functions. For example, time-sensitive cost functions and "implicit submarket closing" can vary the amount of liquidity provided over time, which would be ideal for an outcome space structured over multiple expiration dates.[n] The choice of cost function is also central to the issue of market maker profit and order book depth. With volume-parameterized cost functions, the trade-off between the bid-ask spread and market maker profit can be balanced by diminishing the bid-ask spread as volume increases.[n][n]
The issue of market maker profit raises the critical question, can market participants collectively utilize a decentralized autonomous market maker (DAMM) to provide significant market liquidity? For example, perhaps participants can deposit the funds needed by a DAMM, purchasing a kind of "liquidity bond" that pays returns proportional to trading volume. Alternatively, a DAMM remains minimally funded, serving primarily to calculate unique state clearing prices. In scenarios where the DAM is minimally funded, market liquidity is provided in essentially the same way as in the current market eco-system: by traders independently posting limit orders. But even in this case, the use of batch combinatorial auctions should enhance market liquidity substantially.
5 Conclusion
We began by discussing flaws in the industry standard method of trading related securities on separate order books through independent continuous double auctions, and why those flaws hamper market liquidity and harm trader welfare. Then we explained how to address those flaws with two combinatorial "smart market" mechanisms: (1) batch combinatorial auctions, and (2) automated market makers. And we explained why these mechanisms enhance market liquidity and improve trader welfare. We also presented three explorable examples in the form of interactive charts to help make the concepts more concrete.
The first chart showed how to use combinatorial portfolios of binary options to construct synthetic positions that replicate the payoffs of conventional derivatives. These portfolios are traded as bundles in a combinatorial mechanism, which (by definition) requires a smart market. Thus, the first chart presented an example application to motivate the use of smart market mechanisms. That is, it presented digital currency derivatives as items that can be traded in a smart market, but it did not present the underlying trading mechanisms themselves.
The second and third charts presented the underlying trading mechanisms. The second chart presented a batch combinatorial auction. The third chart presented an automated market maker. These two mechanisms compliment each other; the presence of both enhances liquidity. Broadly speaking, these two mechanisms (an auctioneer and a market maker, respectively) are two of four essential mechanisms that we find in any healthy market (the other two being an issuer and a clearinghouse).
In our presentation of two smart market mechanisms, and example application to digital currency derivatives, several distinct aspects were involved. To summarize, we outline these distinct aspects with four recommendations:
(1) Replace continuous-time serial processing with discrete-time batch processing: Serial processing of bids and offers in continuous-time creates mechanical arbitrage opportunities that are exploited by the fastest traders, leading to an arms race for speed. With batch processing in discrete-time, fast and slow traders alike are on a level playing field, as all traders transact simultaneously at a uniform clearing price. Batch processing with uniform-price clearing forces traders to compete on price rather than use speed to earn arbitrage rents, so bid-ask spreads are reduced. It also encourages traders to place limit orders rather than market orders, since they need not worry about being sniped (overpaying to fast traders). Although we presented batch processing for a combinatorial derivatives market, it can (and should) be applied to conventional double auctions such as spot markets.
(2) Replace independent order books with combinatorial order books: Trading related securities through double auctions on independent order books fragments liquidity and segregates prices. Double auctions are only capable of bilateral order matching, which fragments liquidity and exacerbates the thin market problem. Combinatorial order books enable multilateral matching, unifying liquidity and reducing transaction costs. Segregated prices become irrational in the presence of careless or unsophisticated traders, creating statistical arbitrage opportunities that are exploited by advanced traders. Combinatorial auctioneers can automatically integrate prices so that such arbitrage opportunities never arise, improving the welfare of the average trader.
(3) Construct hedging strategies using combinatorial portfolios of binary options: Hedging strategies that use portfolios of binary options can be traded on combinatorial order books, enabling multilateral matching of hedgers and speculators. Multilateral bid matching aggregates all synthetic positions into a unified pool of liquidity. So regardless of which derivative instrument traders wish to use (such as options, futures, contracts-for-difference, etc.) or what leverage, positions can be combined into complementary sets matched by a combinatorial auctioneer. Thus, the use of combinatorial portfolios aggregates liquidity, enhances leverage and reduces transaction costs.
(4) Use a decentralized autonomous market maker as a default liquidity provider: An on-chain market maker, or decentralized autonomous market maker, acts as a default liquidity provider or “market maker of last resort”. Such on-chain market makers contrast with merely automated market makers that are operated by third-party agents who have no obligations. Without the obligation to stay in a market and to continue providing liquidity when market conditions are volatile, third-party market makers either maximize the bid-ask spread or cancel their orders entirely, precipitating flash crashes. Since on-chain market makers are decentralized autonomous agents guaranteed to execute the instructions specified in source code, they are reliable default liquidity providers.
Appendix
A Stablecoin mechanisms: monetary policy vs. hedging strategies
A full discussion of monetary policy, price stability, and solvency will appear in the long version of this document. For now, we include only a quick-and-dirty comparison between monetary policy and hedging strategies.
A.1 Monetary policy and feedback loops
In brief, stablecoin designs based on monetary policy rely on some estimate of demand, which is used as an input signal to a feedback loop that drives policy decisions. Since the demand is uncertain, a monetary policy scheme is a stochastic control system. And if, for example, price is used as an estimate of demand, then the bid-ask spread is measurement noise. This measurement noise is injected into the system by the policy action, and it may or may not be amplified by the feedback loop. Whether or not the measurement noise is amplified depends on the sensitivity of the transfer function, which is confounded by multiplier uncertainty.
Basically, a stablecoin designer cannot be sure how market participants will react, or if they will overreact, in response to policy decisions. And this holds true regardless of whether the policy decisions are discretionary or non-discretionary (i.e. bureaucratic or algorithmic). From a control theory perspective, it makes little difference because the concern is not the predictability of policy actions, but rather the predictability of how market participants will react in response.
In any case, an important point here is that a more efficient liquidity mechanism will reduce the bid-ask spread and therefore (some of) the measurement noise in a monetary policy feedback loop. Thus, monetary policy also benefits from a better liquidity mechanism, not just hedging strategies. This is NOT to say that more liquidity will necessarily reduce volatility; though it will reduce the transaction costs of hedging volatility. But neither will a dynamic monetary policy necessarily reduce volatility. For instance, if the volume-weighted average price (VWAP) is used as the input signal, and the VWAP is volatile due to low market liquidity, or any other reason besides a true change in demand, then the input signal is mostly measurement noise. In such instances, policy actions would not be driven by an accurate estimate of true demand, but mostly by noise, and volatility would be amplified.
Thus, the claim that an inelastic money supply is the core cause of volatility is misplaced, particularly if speaking about the monetary base (i.e. M0 money). From a control theory perspective, volatility is caused by "genuine uncertainty" due to limited observability, and amplified by a lack of market liquidity. Compared to an open-loop monetary policy (e.g. the bitcoin block reward), a closed-loop monetary policy adds yet another feedback loop into the mix, further complicating the system dynamics. Comparisons to monetary policy at central banks are not very relevant since the low volatility of USD etc. may be due to high liquidity and elastic credit mechanisms (i.e. M1-M3 money), rather than closed-loop monetary policy. In practice, a monetary policy feedback loop may dampen volatility or it may amplify volatility, depending on the level of noise in the signal and how market participants react. In stablecoin models, a closed-loop monetary policy works about as well as the extent to which one makes assumptions about market liquidity and market efficiency (i.e. lack of noise in the input signal and ideal reactions from market participants).
A.2 Quantity theory of money vs. real-world markets
It is intuitively understood that the success of policy actions depends on how market participants will react in response. In particular, monetary policy can be viewed like a string. In an economy undergoing expansion, increasing the supply of money can "pull" down on the currency price. But in an economy undergoing contraction, monetary policy is not effective at increasing demand; it cannot "push" up the currency price, hence "pushing on a string". In the contractionary case, a negative interest rate can help with this Zero lower bound problem to some degree, as a workaround which "pulls" in a negative direction, so to speak. But negative interest rates still only decrease the money supply, they don't actually push up the currency price by stimulating demand.
That monetary policy cannot stimulate demand can be illustrated with a thought experiment in which a stablecoin has a target price peg, and is exchangeable for a volatile reserve asset. If the price of the reserve asset plummets in a negative demand shock, then in theory a negative interest rate on the stablecoin will stimulate the holders to exchange it for the reserve asset, thus reducing the supply of the stablecoin such that (assuming constant demand) its price floats upward back to the peg. But in practice, market participants will respond to a plummeting reserve price by dumping the stablecoin in a sort of "run on the bank" because it is no longer backed by sufficient reserve, causing its peg to break. Such a flight-to-liquidity from the less liquid stablecoin to the more liquid reserve asset (BTC), and from the reserve asset to some even more liquid asset (e.g. USD), triggers a deflationary liquidity trap in which it is not rational for any participant to exchange the volatile reserve asset for the stablecoin.
This thought experiment illustrates the mismatch between the quantity theory of money, which is an ideal model that assumes perfect liquidity, and how participants react in real-world markets. In a system that only has capital inflows (i.e. an expansionary economy), then a peg based on monetary policy should work. But in a system with capital outflows, the peg will break, otherwise the impossible trinity would be violated. Mises stated it succinctly: "It is assumed that, other things being equal, prices must change in proportion to the changes occurring in the total supply of money available. This is not true."
A.3 Money supply: nominal vs. real
Another issue with the monetary policy approach is that it mistakes the nominal number of coins with the money supply, succumbing to the money illusion. If the money supply is instead measured in real terms, then the price of the reserve asset (BTC) becomes a factor, and a more appropriate measure is the market capitalization. In real terms, the money supply is thus constantly adjusting in a continual process of appreciation and depreciation as the market price changes. Thus, measuring the money supply in real terms views the supply as being determined endogenously inthe market process of price discovery. In contrast, a measurement of the money supply in nominal terms views the supply as being determined exogenously by the monetary policy.
Furthermore, monetary policy and hedging strategies can be compared by how their respective feedback processes work. In monetary policy, the market price or some other estimate of demand is used as an input signal to drive a feedback loop which adjusts the nominal coin supply. In such a feedback loop, there is a delay between each signal measurement and the periodic policy action, and the policy action affects the price only indirectly. By comparison, hedging strategies can be seen as adjusting money supply with feedback pressure applied directly on the spot price through the trading mechanism. During expansionary periods, there are more bullish speculators than hedgers, and the feedback is a positive pressure that pushes the spot price higher. During contractionary periods, there are more hedgers than bullish speculators, and the feedback is a negative pressure that pulls the spot price lower.
To elaborate, monetary policy decisions are delayed responses to price signals, whereas hedging strategies exert instantaneous feedback pressure. For example, a monetary policy decision might set a new interest rate, or set a quantity of coins to be sold in a burn auction. But these policy actions occur only after changes in the price signal have been observed; they are delayed responses in a feedback loop. In contrast, hedging strategies exert feedback pressure directly on the price through buying and selling.
In both monetary policy and hedging strategies, the feedback process is affected by the bid-ask spread. In monetary policy, the bid-ask spread is measurement noise in the input signal to a delayed policy decision and action. But with hedging strategies, the bid-ask spread is a transaction cost that directly affects the trading decisions of market participants. Such a transaction cost can be viewed as an "interest rate" that is factored into the purchase price of a stable-portfolio beforehand. For example, during periods of expansion there will be more demand for bullish positions than bearish positions. So we can expect the purchase price of a stable-portfolio to be less than the face-value of the payoff, say a $97 cost to purchase a $100 stable-portfolio. Thus, hedgers receive a $3 discount on their short positions, in effect earning a 3% interest rate, which is paid by bullish speculators as a premium for taking long positions. During contractionary periods the equilibrium is reversed; the purchase price of a stable-portfolio will be greater than the face-value of the payoff, with a negative interest rate effectively priced in. For instance, purchasers of stable-portfolios might pay $103 for $100 of stable-value, in effect paying a 3% negative interest rate or premium. The premium paid by hedgers is received by bullish speculators as a discount on their long positions, for their willingness to lend reserve to the hedgers taking short positions.
A.4 Open market operations for price pegs
The hedging strategy that we describe is similar to some monetary policy schemes in that a sort of "central bank" performs open market operations.[n] Possible open market operations for a stablecoin mechanism include conducting "burn auctions" or setting interest rates on deposits. In the hedging strategy that we describe, the decentralized autonomous market maker (DAMM) buys and sells portfolios of derivative contracts, holding reserve (BTC) until payout when the contracts expire. This buying and selling can be viewed as performing open market operations with the goal of defending a peg within a band, where the band is the outcome space of future BTC/USD spot prices. The outcome space specifies an upper and lower bound on the spot price, and as long as the spot price is within this band, the derivative "stable-portfolios" are essentially pegged to a stable value. Furthermore, the DAMM defends a peg only until some expiration date, e.g. three months after the market opens. After a market expires, a new market is initialized with a new expiration date and new upper and lower bounds on the outcome space. In this way, stable-portfolios can be viewed as crawling pegs over a sequence of bands and expiration dates. Crucially, the DAMM can only defend the peg to the extent that it is funded with "reserve". Once all of the DAMM's funds are allocated and the spot price is near either the upper or lower bound of the band, it can no longer effectively provide liquidity to defend the peg.
On the whole, monetary policy schemes and hedging strategies are more similar than different. They are similar because both ultimately rely on the availability market liquidity, and both seek to transform volatility into stability. They are different in that monetary policy tries to stabilize price, whereas a hedging strategy tries to stabilize value. Furthermore, monetary policy scheme measures money supply in nominal terms, while hedging strategies measure money supply in real terms.
The two can also be distinguished by comparing the promises or guarantees they provide when it comes to exchanging the stable-value asset for the volatile reserve asset and vice versa. In some monetary policy schemes (e.g. SchellingDollar), the reserve asset can be exchanged for the stable-value asset at the pegged rate at any time. But there is no guarantee on the rate received when redeeming the stable-value asset for the volatile reserve asset, since it is left to market forces. Thus, the peg is based on assumptions of market liquidity in the future, and how participants will respond to policy actions in the meantime.
In contrast, hedging strategies offer no guarantees on the rate for the initial exchange from volatile reserve asset to stable-valued asset, leaving market forces to determine such transaction costs. But since hedging strategies hold and allocate "reserve" in a collateralized contract, they guarantee that the stable-asset can be redeemed for the full face-value at the time of contract expiration regardless of how market participants act in the meantime. Although to be fair, the guarantee of full face-value redemption is conditioned on the price of the reserve being within the band limits set by the hedging contract.
Acknowledgements
Thanks to Chris Hibbert for discussions about automated market makers and bundle matching, and feedback on example charts; Steve Waldman for discussion about market making and cryptoassets; Matt Liston for discussions about combinatorial mechanisms; and Ming Chan and caktux for discussions and feedback on example charts.
Notes
References



